HAWASSI –AB1:
Analytic Boussinesq Model (1HD)
Fast simulation of fully dispersive, high-order nonlinear and breaking waves
HAWASSI-AB for fast simulations of high, very nonlinear, breaking or non-breaking waves in 1HD (long crested), with the capacity to obtain reliable statistics about extreme wave occurrence in reasonable short time. The interior fluid motion is modelled in an analytic way using Fourier-Integral Operators; as a consequence, dispersive properties are modelled exactly. Nonlinear effects can be included to any order, implemented until 4th-order. Breaking waves are modelled using an eddy-viscosity method with kinematic breaking criterion.
Features of the 1HD code include
- Waves of any wave length can be simulated in coastal and oceanic waters
- Varying bottom is accommodated, including run-up
- Various methods for wave influx from multiple interior positions
- Use of efficient damping zones and (partially reflecting) walls
- Interior Flow Module for the calculation of interior fluid velocities, fluid accelerations and the (dynamic and total) pressure at user defined positions between surface and bottom
Facilities of the software include
- GUI for input of wave characteristics and model parameters, and GUI for post-processing
- Time partitioned simulation is possible to reduce hardware requirements
- Project examples with harmonic, focusing and irregular waves above bathymetry in various geometries
- Manual for easy operation and scientific description of the equations with literature references
Just like HAWASSI-VBM, AB is based on the following principles
- The free surface dynamics for inviscid, incompressible fluid is governed by a set of Hamilton equations for the surface elevation
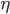 and the potential
and the potential 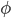 at the surface.
at the surface. - By approximating the kinetic energy functional
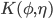 explicitly as an expression in
explicitly as an expression in 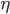 , and
, and 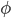 , the simulation of the interior flow can be avoided, the Boussinesq character of the codes.
, the simulation of the interior flow can be avoided, the Boussinesq character of the codes. - The way of approximating
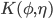 is based on Dirichlet’s principle for the boundary-value problem in the fluid domain. By restricting the set of competing functions in the minimization, an approximation of
is based on Dirichlet’s principle for the boundary-value problem in the fluid domain. By restricting the set of competing functions in the minimization, an approximation of 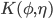 is obtained. The variational derivative
is obtained. The variational derivative  is the corresponding consistent approximation of the Dirichlet-to-Neumann operator.
is the corresponding consistent approximation of the Dirichlet-to-Neumann operator. - The (approximate) Hamilton system conserves the (approximate) positive definite total energy exactly, avoiding sources of instability.
The time dynamics is explicit, no CFL-conditions are required. Time stepping is done with matlab ode45 code, with automatic variable time step.
In AB 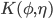 is calculated using a generalization of the linear Airy-interior potential; the generalization takes into account varying bottom and surface elevation. The generalization can deal with arbitrary bottom and has flexible order of nonlinearity for the surface elevation.
is calculated using a generalization of the linear Airy-interior potential; the generalization takes into account varying bottom and surface elevation. The generalization can deal with arbitrary bottom and has flexible order of nonlinearity for the surface elevation.
Implementation
- Fourier-integral operators (FIO) are used in a spatial-spectral implementation.
- The FIO’s are approximated to enable efficient FFT-methods by interpolation techniques.
- Localization methods have been implemented to deal with walls, breaking waves, etc.
- AB, using Fourier methods, has uniform spatial grid step, independent on local depth.
Download the demo version of HAWASSI-AB
Download the manual of HAWASSI-AB1
Dam break problem
Simulation of wave run-up and breaking
Wave design for wave tank experiments
Irregular wave simulations vs experiment

