HAWASSI – VBM Variational Boussinesq Model
Finite Element implementation with Optimized Dispersion
Application Areas
- HAWASSI – VBM1 for (1HD) simulations of irregular waves in wave tanks above flat and varying bottom.
- HAWASSI – VBM2 for (2HD) simulations with short-crested waves in coastal areas with harbours and strongly varying bathymetry, and for simulation of oceanic waves.
The interior fluid motion is modelled by a combination of a few (Airy-type) depth profiles; this makes it possible to optimize the dispersion properties depending on the specific case to be simulated. Nonlinear effects are accounted for in a weakly nonlinear way that is sufficient for most applications.
Features of the 1&2HD code include
- The quality of dispersion is optimized for the specific wave problem to be simulated, which makes it possible to simulate deep ocean waves or very short waves (kh=15 or more) and infragravity waves
- Use of an unstructured grid with mesh-size depending on bathymetry
- Various methods for wave influx from multiple interior lines using sources in the dynamic equations
- Use of efficient damping zones, (partially reflecting) walls for harbour lay-outs, etc
- Interior Flow Module for the calculation of interior fluid velocities, fluid accelerations and the (dynamic and total) pressure at user defined positions between surface and bottom
Facilities of the software include
- GUI for input of wave characteristics and model parameters, GUI for post processing
- For VBM2 easy generation by using a GUI of an unstructured mesh based on local depth for given bathymetry and geometric structures
- Time partitioned simulation is possible to reduce hardware requirements
- Project examples with harmonic, focusing and irregular waves above bathymetry in various geometries
- Manual for easy operation and scientific description of the equations with literature references
Underlying Modelling Methods
Just like HAWASSI-AB, VBM is based on the following principles
- The free surface dynamics for inviscid, incompressible fluid is governed by a set of Hamilton equations for the surface elevation
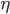 and the potential
and the potential 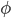 at the surface.
at the surface. - By approximating the kinetic energy functional
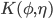 explicitly as an expression in
explicitly as an expression in 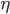 , and
, and 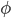 , the simulation of the interior flow can be avoided, the Boussinesq character of the codes.
, the simulation of the interior flow can be avoided, the Boussinesq character of the codes. - The way of approximating
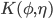 is based on Dirichlet’s principle for the boundary-value problem in the fluid domain. By restricting the set of competing functions in the minimization, an approximation of
is based on Dirichlet’s principle for the boundary-value problem in the fluid domain. By restricting the set of competing functions in the minimization, an approximation of 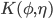 is obtained. The variational derivative
is obtained. The variational derivative  is the corresponding consistent approximation of the Dirichlet-to-Neumann operator.
is the corresponding consistent approximation of the Dirichlet-to-Neumann operator. - The (approximate) Hamilton system conserves the (approximate) positive definite total energy exactly, avoiding sources of instability.
The time dynamics is explicit, no CFL-conditions are required. Time stepping is done with matlab ode45 code, with automatic variable time step.
In VBM the interior flow is approximated by using a linear combination of vertical Airy profiles, characterized by the values of wave numbers 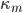 . The choice of these values determines the dispersion relation. Given the spectrum of the influx signal (or initial profile) of the case under investigation, the values of
. The choice of these values determines the dispersion relation. Given the spectrum of the influx signal (or initial profile) of the case under investigation, the values of 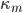 are optimized for best performance for the relevant frequency interval. Therefore, VBM can have excellent, tailor-made, dispersive properties; deep water waves can be simulated just as well as infragravity waves.
are optimized for best performance for the relevant frequency interval. Therefore, VBM can have excellent, tailor-made, dispersive properties; deep water waves can be simulated just as well as infragravity waves.
Implementation
A Finite Element method using piece-wise linear splines can deal with the first order differentiations that appear in the approximate KE. In addition a system of elliptic equations in the horizontal variables has to be solved for the amplitudes of the Airy functions. VBM uses variable grid size depending on the local depth, making 2HD simulations more efficient.
Download the demo version of HAWASSI-VBM
Download the manual of HAWASSI-VBM1
Download the manual of HAWASSI-VBM2
Optimal (re-) design of harbours and breakwaters
Pre-design of experiments in wave tanks to test ships
Simulation of irregular waves entering a harbour
Harbour assessment
Wave design for wave tank experiments
Irregular wave simulations vs experiment

